Aril and Dita are wealthy Norwegian business owners who make monthly donations to international disaster relief.
- Aril donated 150 Norwegian kroner (KR ) the first month and the cumulative number of Norwegian kroner she has donated increases by a factor of 2.5 each month.
- Dita donated 300 KR the first month and the cumulative number of Norwegian kroner she has donated increases by 400 KR each month.
They started making donations at the same time, and they both make their monthly donations at the beginning of each month.
What is the first month in which Aril’s cumulative donation exceeds Dita’s cumulative donation?
Exponential growth is a growth whose rate is rapid in proportion to the function’s current value. Linear growth is a growth whose rate is constant over time.
Based on the context, we can say that Aril’s donation is an exponential growth and can be model by an equation:
y = 150 * (2.5)^(x-1)
And Dita’s donation is a linear growth and can be modeled as:
y = 300 + 400(x-1)
Why (x-1)? Because in the first month which is x, Aril and Dita have already donated 150 KR and 300 KR respectively. Therefore, we have to subtract the first month to know the rate of the following months.
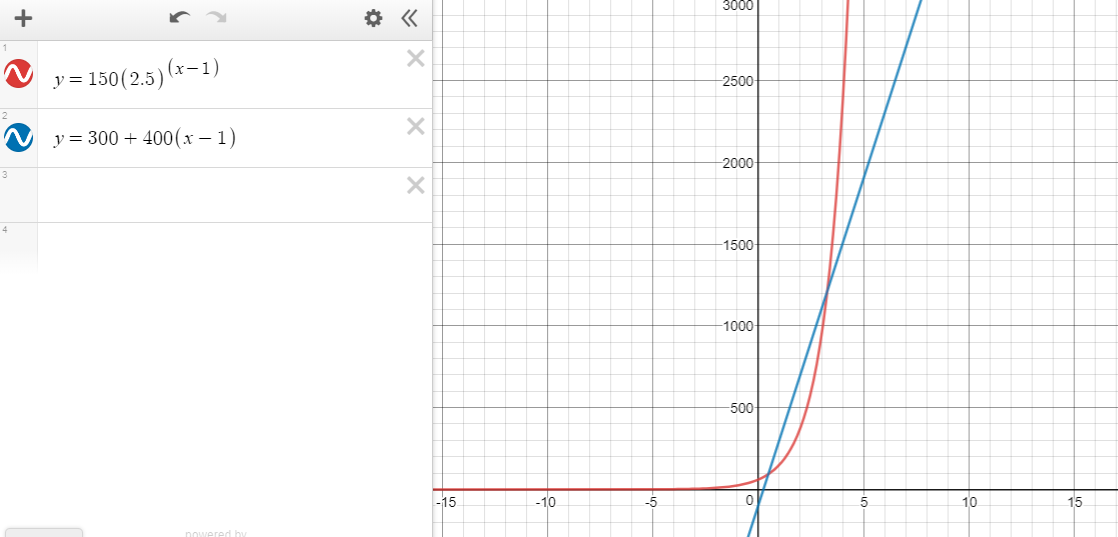
Now, let’s figure out which month Aril’s donation exceeds Dita’s donation. Let’s think of it graphically.
We know that exponential growth started off slowly and will eventually outreach linear growth; therefore, we have to look for its intersection.
The two lines intersect at 3.28, 1212.17. Therefore, we can conclude that at month 4, Aril’s donation will exceed Dita’s.
What is the first month in which Aril’s cumulative donation exceeds Dita’s cumulative donation?